الدوال المثلثية

كتابة:
الدوال المثلثية

الدوال المثلثية

الدوال المثلثية من أهم محاور علم المثلثات والذي يعد أحد فروع الرياضيات الذي يهتم بالزوايا وتطبيقها على الحسابات، وهناك ست دوال مثلثية في علم المثلثات هي الجيب (Sin) وجيب التمام (Cos) والظل (Tan) وظل التمام (Cot) والقاطع (Sec) وقاطع التمام (Csc)، وقد تم اشتقاق هذه الدوال المثلثية الست بالنسبة إلى المثلث قائم الزاوية، وقد تطور علم المثلثات بسبب الحاجة لحساب الزوايا والمسافات في مجالات علمية عديدة مثل علم الفلك ورسم الخرائط والمسح واكتشاف نطاق المدفعية.[١]

الصيغ الأساسية للدوال المثلثية

هناك ست دوال مثلثية أساسية مستخدمة في علم المثلثات هي الجيب وجيب التمام والقاطع وقاطع التمام والظل وظل التمام، حيث إن الدوال المثلثية هي نسبة أضلاع مثلث قائم الزاوية إلى بعضها وهي الضلع العمودي والوتر والقاعدة، حيث يتم إيجاد قيمة الدوال المثلثية بالاستناد لأضلاع المثلث القائم وفق الصيغ التالية:[٢]

  • جيب الزاوية (sin θ): وهو ناتج قسمة قيمة الضلع المقابل للزاوية على قيمة وتر المثلث القائم (sin θ = Perpendicular/Hypotenuse)
  • جيب التمام للزاوية (cos θ): وهو ناتج قيمة قسمة الضلع المجاور للزاوية على قيمة وتر المثلث القائم (cos θ = Base/Hypotenuse)
  • ظل الزاوية (tan θ): وهو ناتج قسمة قيمة الضلع المقابل للزاوية على قيمة الضلع المجاور لها (tan θ = Perpendicular/Base)
  • قاطع الزاوية (sec θ): وهو ناتج قسمة قيمة وتر المثلث قائم الزاوية على قيمة الضلع المجاور لها (sec θ = Hypotenuse/Base)
  • قاطع تمام الزاوية (cosec θ): وهو ناتج قسمة قيمة وتر المثلث قائم الزاوية على قيمة الضلع المقابل لها (cosec θ = Hypotenuse/Perpendicular)
  • ظل تمام الزاوية (cot θ): وهو ناتج قسمة قيمة الضلع المجاور للزاوية على قيمة الضلع المقابل لها (cot θ = Base/Perpendicular)


قيم الدوال المثلثية للزوايا الرئيسية

تمثل الاقترانات الجيب وجيب التمام والظل الاقترانات الأساسية في علم المثلثات والتي يمكن اشتقاق الدوال الثلاثة ظل التمام والقاطع القاطع والتمام منها وغالبًا ما تُستخدم الاقترانات الثلاثة المشتقة في عملية مقارنة بالوظائف المثلثية الأولية، وقيم الدوال المثلثية للزاويا الست المشهورة (°90 و°60 و°45 و°30 و°0) هي.[٣]


النسب المثلثية (Trigonometric Ratios)
0 °
30 °
45 ° 
60 ° 
90 °
جيب الزاوية (Sin θ)
0
1/2
1/√2
√3/2
1
جيب تمام الزاوية (Cos θ)
1
√3/2
1/√2
1/2
0
ظل الزاوية (Tan θ)
0
1/√3
1
√3
∞
قاطع تمام الزاوية (Cosec θ)
∞
2
√2
2/√3
1
قاطع الزاوية (Sec θ)
1
2/√3
√2
2
∞
ظل تمام الزاوية (Cot θ)
∞
√3
1
1/√3
0


المجال والمدى للرسوم البيانية الخاصة بالدوال المثلثية

حتى يتم إنشاء رسم بياني صحيح للدوال المثلثية يجب معرفة قيمة المجال والمدى لكل دالة، وهذه القيم التي سيتم رسمها في المستوى XY وهي:[٣]


الدالة (Function)
تعريف الدالة (Definition)
المجال (Domain)
المدى (Range)
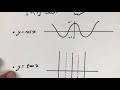
اقتران جيب (Sine Function)
y=sin x
x ∈ R
− 1 ≤ sin x ≤ 1
اقتران جيب التمام(Cosine Function)
y = cos x
x ∈ R
− 1 ≤ cos x ≤ 1
اقتران الظل (Tangent Function)
y = tan x
x ∈ R , x≠(2k+1)π/2,
− ∞ < tan x < ∞
اقتران ظل التمام (Cotangent Function)
y = cot x
x ∈ R , x ≠ k π
− ∞ < cot x < ∞
اقتران القاطع (Secant Function)
y = sec x
x ∈ R , x ≠ ( 2 k + 1 ) π / 2
sec x ∈ ( − ∞ , − 1 ] ∪ [ 1 , ∞ )
اقتران قاطع التمام (Cosecant Function)
y = csc x
x ∈ R , x ≠ k π
csc x ∈ ( − ∞ , − 1 ] ∪ [ 1 , ∞ )


المتطابقات المثلثية

فيما يلي أهم المتطابقات المتعلقة بدوال حساب المثلثات:[٣]


المتطابقات الزوجية والفردية

الدالتان جتا (cos) وقاطع الزاوية (sec) هما دالاتان زوجيتان، أما باقي الدوال المثلثية فهي دوال فردية، أي أن قيمها تكون على الشكل التالي:[٣]

  • sin(-x) = -sin x
  • cos(-x) = cos x
  • tan(-x) = – tan x
  • cot(-x) = -cot x
  • csc(-x) = -csc x
  • sec(-x) = sec x


متطابقات فيثاغورس

يتم التعبير عن نظرية فيثاغورس باستخدام الدوال المثلثية من خلال المتطابقات التالية:[٣]

  • sin^2 x + cos^2 x = 1
  • 1 + tan^2 x = sec^2 x
  • cosec^2 x = 1 + cot^2 x


الاقترانات الدورية

الاقترانات المثلثية هي اقترانات دورية، وتكون أصغر دورة دورية هي 2π لكن بالنسبة للظل وظل التمام فهي π، والإقترانات الدورية هي:

  • sin(x+2nπ) = sin x
  • cos(x+2nπ) = cos x
  • tan(x+nπ) = tan x
  • cot(x+nπ) = cot x
  • csc(x+2nπ) = csc x
  • sec(x+2nπ) = sec x


حيث إن n هو أي عدد صحيح.


متطابقات المجموع والفرق

  • sin(x+y) = sin(x).cos(y)+cos(x).sin(y)
  • sin(x–y) = sin(x).cos(y)–cos(x).sin(y)
  • cos(x+y) = cosx.cosy–sinx.siny
  • cos(x–y) = cosx.cosy+sinx.siny
  • tan(x+y) = [tan(x)+tan(y)]/[1-tan(x)tan(y)]
  • tan(x-y) = [tan(x)-tan(y)]/[1+tan(x)tan(y)]

المراجع

  1. ↑ Raymond Walter Barnard, "trigonometry", britannica, Retrieved 5/1/2022. Edited.
  2. ↑ "Trigonometric Functions", cuemath, Retrieved 5/1/2022. Edited.
  3. ^ أ ب ت ث ج "Trigonometric Functions", byjus, Retrieved 5/1/2022. Edited.
4463 مشاهدة
للأعلى للسفل
×