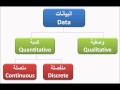
مبادئ الإحصاء الوصفي
يعدّ علم الإحصاء (بالإنجليزية: statistics) أحد أهم فروع علم الرياضيات، والذي بدوره يتكون من قسمين رئيسين هما؛ الإحصاء الوصفي والإحصاء الاستدلالي، حيث يعد الإحصاء الوصفي لب التحليل الكمي، وهو طريقة علمية لوصف وتلخيص البيانات ذات الأهمية بطرق واضحة ومفيدة وتكمن أهميته في توفير المعلومات الأساسية حول متغيرات معينة من ضمن مجموعة بيانات.[١]
يعد الوسط الحسابي من الأمثلة المهمة على الإحصاء الوصفي، حيث يتم استخدام الوسط الحسابي لوصف توزيع البيانات والمتغيرات المقاسة على فترات زمنية أو نسب معينة وفي هذا المقال سيتم توضيح مبادئ الإحصاء الوصفي.[١]
لمعرفة المزيد يمكنك قراءة المقال الآتي: تعريف الإحصاء الوصفي.
الهدف من مبادئ الإحصاء الوصفي هو تلخيص مجموعة من الملاحظات واستنباط التنبؤات أو القرارات حول مجموعة من البيانات بناءً على المعلومات الواردة في عينة منها، وتحديد مستوى التباين فيها ويقوم علم الإحصاء الوصفي على مبدأين رئيسين لوصف البيانات وهما كالآتي:
مقاييس النزعة المركزية
هي إحصائية موجزة تمثل النقطة المركزية أو القيمة النموذجية لمجموعة البيانات، وتعد المبدأ الأول من مبادئ الإحصاء الوصفي، وتشير هذه المقاييس إلى المكان الذي تقع فيه معظم القيم في البيانات ويشار إليها كذلك بالموقع المركزي للبيانات، ويمكن القول أنها ميل البيانات للتجمع حول قيمة متوسطة.
لمعرفة المزيد يمكنك قراءة المقال الآتي: مقاييس النزعة المركزية.
وفيما يأتي أهم مقاييس النزعة المركزية: [٢]
- الوسط الحسابي: هو المقياس الأكثر شيوعًا واستخدامًا في جميع المجالات العلمية والعملية، وتعد عملية قياس الوسط الحسابي عملية بسيطة جدًا، إذ يتم بالخطوة الأولى جمع كل القيم وفي الخطوة الثانية يتم تقسيم مجموع القيم على عددها للحصول على الوسط الحسابي لمجموعة من القيم.
لمعرفة المزيد يمكنك قراءة المقال الآتي: قانون الوسط الحسابي.
- الوسيط: هو القيمة التي تقع في منتصف توزيع البيانات عندما يتم ترتيب هذه البيانات ترتيبا تصاعديًا، أي من القيمة الأدنى إلى القيمة الأعلى، ويتم استخدام الوسيط للمتغيرات التي تقاس بأفضلية معينة أو نسب، ولحساب الوسيط يتم ترتيب البيانات ترتيبًا تصاعديًا ثم اختيار القيمة التي تقع في منتصف القيم كقيمة الوسيط، وفي حال كان عدد البيانات زوجيًا عند ترتيبها يتم أخذ المتوسط الحسابي للقيمتين اللتين تقعان في منتصف القيم.
لمعرفة المزيد يمكنك قراءة المقال الآتي: ما هو الوسيط.
- المنوال: هو المقياس الذي يحدد القيمة أو المتغير الذي يحدث بشكل متكرر في توزيع البيانات، ويمكن حساب المنوال لأي نوع من البيانات سواء كانت عددية أو نوعية، بما في ذلك البيانات المقاسة كمتغيرات اسمية، ومن الجدير بالذكر أنّ هناك بيانات ليس لديها منوال أبدًا، ويحدث هذا عندما يكون التكرار لجميع القيم متساوٍ ويتم حساب المنوال بإيجاد تكرار كل قيمة واختيار القيمة الأكثر تكرارًا كقيمة المنوال.
لمعرفة المزيد يمكنك قراءة المقال الآتي: كيفية حساب المنوال.
مقاييس التشتت
هي ثاني مبادئ الإحصاء الوصفي، وتعرف مقاييس التباين بأنّها الكميات التي تعبر عن مقدار الاختلاف في متغير عشوائي، ويوصف التباين أحيانًا بأنّه انتشار أو تشتت، ومن الجدير بالذكر أن مقايس التباين؛ هي إما خصائص لتوزيع الاحتمالات أو تقديرات لعينات منها، و من أهم مقاييس التباين: [٣]
- التباين: هو الفرق بين القيمة الأكبر والأصغر، وهو متوسط مربع الفرق بين متغير عشوائي ومتوسطه، ويعد ذا أهمية أساسية في التحليل الإحصائي.
- الانحراف المعياري: هو الجذر التربيعي للتباين، ويحتوي الانحراف المعياري على نفس وحدات القياس مثل الوسط.
لمعرفة المزيد يمكنك قراءة المقال الآتي: مقاييس التشتت في الإحصاء.
المراجع
- ^ أ ب "What Is Descriptive Statistics? - Examples & Concept", study.com, Retrieved 15-1-2021. Edited.
- ↑ "The Difference Between the Mean, Median, and Mode", www.thoughtco.com, Retrieved 15-1-2021. Edited.
- ↑ "measures of variation", www.encyclopedia.com, Retrieved 15-1-2021. Edited.