شرح البوابات المنطقية المشتقة وأمثلة عليها

كتابة:
شرح البوابات المنطقية المشتقة وأمثلة عليها

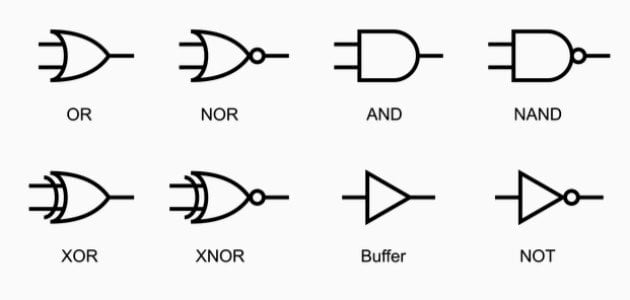
بوابة NAND

تعمل بوابة NAND على عكس مخرجات بوابة AND وهي إختصار لـ AND NOT أي نفي ال AND، وتتشكل بوابه NAND بتوصيل مخرج بوابة AND  بمدخل بوابة NOT، بوابة عالمية في مجال الإلكترونيات ومفيدة للغاية لأنها تستطيع بناء أي دائرة منطقية بسيطة أو معقدة باستخدام بوابات NAND فقط.[١]


يُشار إلى التعبير المنطقي لبوابة NAND المنطقية بنقطة واحدة وهي التي تدل على الAND (.) مع خط علوي (‾‾) فوق التعبير للدلالة على NOT أو النفي المنطقي لبوابة NAND.[١]


كما وتمثل بالمعادلة التالية: `(A.B).[١] لنفرض أن المدخلات ممثلة بالقيم A,B:[١]

  • الخطوة الأولى: سيكون ناتج ال AND بينهما أي A.B يساوي واحدًا في حال كان احد المدخلات يساوي صفرًا.
  • الخطوة الثانية سيكون  NOT أو نفي الناتج السابق.

‾‾: تدل هذه العلامة على النفي كما وأيضاً العلامة ` أو ~ .


جدول الحقيقة لبوابة NAND   

يمثل هذا الجدول ناتج أو قيمة المخرج أو ما يعرف بال (Output) لكل مدخل منطقي أو (Input) محتمل على حدىً، فهو يعمل على وصف السلوك لهذه البوابة المنطقية أو الدائرة المنطقية، وبصفة عامة فإنه يستخدم كخريطة كارنو فايتش أو(karanaugh map) وكما في الجدول التالي وهو في حالة وجود مدخلين فقط:[٢]
Read as A AND B gives NOT Q
Q
B
A
1
0
0
1
1
0
1
0
1
0
1
1


المعلومات المتعلقة بطريقة حساب ناتجها تأتي كالتالي:[٢]

  • تكون مخرجات جميع بوابات NAND 0 فقط في حالة واحدة وهي أن تكون جميع المدخلات تساوي 1.
  • تكون مخرجات جميع بوابات NAND عالية أو 1 دائماً في ما سوى الحالة السابقة.


الرمز أو الشكل عبارة عن بوابة AND  مع دائرة صغيرة في جهة المخرجات وهي التي تمثل الدائرة الانعكاس أو النفي كما تظهر في الصورة:[٢]

قد يزيد عدد المدخلات ولكن الناتج مخرج واحد وقيمة واحدة في جميع الأحوال.[٢]


أمثلة على بوابة NAND

من الأمثلة على بوابة NAND ما يأتي:

مثال:1

  • 1 NAND 1
  • `(1.1)
  • 0=`1


مثال:2

  • (1 NAND 1) NAND 1
  • (1.1)` NAND 1
  • 0 NAND 1
  • (1.0)`
  • 1


بوابة NOR

تعمل بوابة NOR على عكس مخرجات بوابة OR، وهي إختصار لـ NOT OR أي نفي ال OR، وتتشكل بوابه NOR بتوصيل مخرج بوابة OR بمدخل بوابة NOT.[٣]


ويُشار إلى التعبير المنطقي لبوابة NOR بعلامة زائد (+) تدل على ال OR مقرونة بخط علوي (‾‾) فوق التعبير للدلالة على NOT أو النفي المنطقي لبوابة NOR كالاتي:[٢]

كما وتمثل بالمعادلة التالية: `(A+B).


المعلومات المتعلقة بطريقة حساب ناتجها تأتي كالتالي:[٣]

  • تعطي البوابة NOR الناتج 0 إذا كانت قيمة أحد المدخلين أو كليهما تساوي 1.
  • تعطي الناتج 1 إذا كانت المداخل جميعها تساوي 0.
  • قد يزيد عدد المدخلات ولكن الناتج مخرج واحد وقيمة واحدة في جميع الأحوال.


جدول الحقيقة لبوابة NOR

يمثل هذا الجدول ناتج أو قيمة المخرج أو ما يعرف بال (Output) لكل مدخل منطقي أو (Input) محتمل على حدى فهو يعمل على وصف السلوك لهذه البوابة المنطقية أو الدائرة المنطقية، وبصفة عامة فإنه يستخدم كخريطة كارنو فايتش أو(karanaugh map) وكما في الجدول التالي وهو في حال وجود مدخلين فقط:[٣]
Read as A OR B gives NOT Q
Q
A
B
1
0
0
0
1
0
0
0
1
0
1
1


أمثلة على بوابة NOR

من الأمثلة على بوابة NOR ما يأتي:

مثال:1

  • 1 NOR 1
  • =0


مثال:2

  • (1 NOR 1) NOR 1
  • = (1+1)` NOR 1
  • = 0 NOR 1
  • (0+1)`
  • 0 =


بوابة XOR

تُستخدم البوابة المنطقية XOR بشكل كبير في الدوائر الرقمية لمعالجة الإشارات التي تمثل الأرقام الثنائية (Binary)، يطلق عليها الأسماء EOR، EXOR، وهي بوابة منطقية متعددة المداخل ولها مخرج واحد، وتُستخدم على نطاق واسع في عملية التشفير، يتم تمثيلها عادةً بالرمز ⊕. [٤]


المعلومات المتعلقة بطريقة حساب ناتجها تأتي كالتالي:[٤]

  • يكون المخرج 1 فقط عندما يكون أحد المدخلات 1.
  • عندما يكون كلا المدخلين متساويان، كأن يكون كلاهما 1 أو كلاهما 0، فيكون الناتج 0.


تقوم البوابة المنطقية XOR على المعادلة المنطقية التالية: A.~B+~A.B أو (A+B).( ~A+~B)، وتتمثل بالشكل التالي:[٥]


جدول الحقيقة لبوابة XOR

يمثل هذا الجدول ناتج أو قيمة المخرج أو ما يعرف بال  (Output) لكل مدخل منطقي أو (Input) محتمل على حدى فهو يعمل على وصف السلوك لهذه البوابة المنطقية أو الدائرة المنطقية، وبصفة عامة فإنه يستخدم كخريطة كارنو فايتش أو(karanaugh map) وكما في الجدول التالي وهو في حالة وجود مدخلين فقط:[٥]
2-input XOR Gate:
Q
B
A
0
0
0
1
1
0
1
0
1
0
1
1


أمثلة على بوابة XOR

من الأمثلة على بوابة XOR ما يأتي:

مثال:1

  • (1 XOR 1) XOR 1
  • 0 XOR 1
  • =1


مثال:2

افرض أن

  • : A = 1, B = 0
  • A XOR B
  • 1.0` + 1`.0 = 1+0 = 1


بوابة XNOR

تعمل بوابة XNOR على عكس دالة XOR، وهي اختصار من (Exclusive NOR) حيث (NOR) تعني (NOT XOR)، ولهذه البوابة مدخلان ومخرج واحد،[٦]تقوم البوابة المنطقية XNOR على المعادلة المنطقية التالية:[٦]

A.B +~A.~B أو مكافئتها (A+~B).(~A+B) 


المعلومات المتعلقة بطريقة حساب ناتجها تأتي كالتالي:[٦]

  • تكون قيمة الناتج تساوي واحدًا في حال تساوي قيم المداخلات.
  • تكون قيمة الناتج تساوي صفرًا في حال اختلاف قيم المداخلات.


تمثّل هذه القيمة نتاج عملية النفي NOT للقيمة الناتجة من تطبيق بوابة XOR على المدخلات، ورمزها (Q =(A ⊕ B)' وتسمى أيضاً ENOR وتمثل بالصورة أو الشكل التالي:[٦]


جدول الحقيقة لبوابة XNOR

يمثل هذا الجدول ناتج أو قيمة المخرج أو ما يعرف بال (Output) لكل مدخل منطقي أو (Input) محتمل على حدى فهو يعمل على وصف السلوك لهذه البوابة المنطقية أو الدائرة المنطقية، وبصفة عامة فإنه يستخدم كخريطة كارنو فايتش أو(karanaugh map) وكما في الجدول التالي وهو في حالة وجود مدخلين فقط:[٧]
2-input XNOR Gate:
Q
B
A
1
0
0
0
1
0
0
0
1
1
1
1


أمثلة على بوابة XNOR

من الأمثلة على بوابة XNOR ما يأتي:

مثال:1

  • 1 XNOR 1
  • A.B +~A.~B
  • 1.1 +~1.~1
  • 1+0
  • 1 =


مثال:2

  • (1 XNOR 1) XNOR 1
  • A.B +~A.~B
  • = 1.1 +~1.~1 XNOR 1
  • = 1 XNOR 1
  • 1.1 +~1.~1
  • 1+0
  • 1 =


تدريبات على البوابات المشتقة

تدريبات على NAND

تاليًا أهم التدريبات على NAND:

مثال:1

  • (1 NAND 1) or 0
  •  0 OR 0
  • 0 =


مثال:2

  • (1 NAND 0) and 1
  •  1 and 1
  • 1 =


مثال:3

  • C=0 ، B=1 ، A=1
  • NOT (NOT (A NAND B) NAND C
  • NOT (NOT (1 NAND 1) NAND 0
  • NOT (NOT (0) NAND 0
  • NOT (NOT 1)
  • NOT (0)
  • 1=


تدريبات على NOR

تاليًا أهم التدريبات على NOR:

مثال:1

  • (1 NOR 1) or 0
  •  0 OR 0
  • 0


مثال:2

  • (1 NOR 0) and 1
  •  0 and  1
  • 0


مثال:3

  • D=0،C=0 ، B=1 ، A=1
  • NOT (NOT (A NOR B) NOR C NOR D)
  • NOT (NOT (1 NOR 1) NOR 0 NOR 0)
  • NOT (NOT (0) NOR 0 NOR 0)
  • NOT (1 NOR 1)
  • NOT (0)
  • 1 =


تدريبات على XOR

تاليًا أهم التدريبات على XOR:

مثال:1

افرض أن:

  • A = 0, B = 0
  • A XOR B
  • 0.0` + 0`.0 = 0+0
  • = 0


تدريبات على XNOR

تاليًا أهم التدريبات على XNOR:

مثال:1

  • (1 XNOR 1) or 0
  •  1 OR 0
  • 1 =


مثال:2

  • (1 XNOR 0) and 1
  •  0 and 1
  • 0 =


مثال:3

  • ،C=0 ، B=1 ، A=1
  • NOT (NOT (A XNOR B) XNOR C )
  • NOT (NOT (1 XNOR 1) XNOR 0)
  • NOT (NOT (1) XNOR 0)
  • NOT (NOT 0 )
  • NOT (1 )
  • 0 =


الخلاصة

البوابات المنطقية هي الأساس لأي نظام رقمي، فهي عبارة عن دائرة إلكترونية بها مدخل واحد أو أكثر ومخرج واحد فقط، وتقوم العلاقة بين المدخلات والمخرجات على أسس معينة تختلف من واحدة لأخرى وبناءً عليه تسمى بالأسماء المختلفة كبوابة AND أو بوابة OR أو بوابة NOT وغيرها من البوابات الرئيسة.[٨]


تعمل هذه البوابات على تحويل القيم إلى لغة الحاسوب بالاستعانة بأنظمة العد المختلفة ومن ثم القيام بمعالجتها لإظهار النتائج، وكل ما ذكرناه سابقاَ من البوابات المنطقية هي اشتقاق من بوابات منطقية رئيسة، فبوابة الNAND هي اشتقاق من البوابة الرئيسية AND، وكل من: NOR  , XNOR XOR هي اشتقاق من البوابة الرئيسية OR.[٨]

المراجع

  1. ^ أ ب ت ث Doug Lowe, "Electronics Logic Gates: Universal NAND Gates", dummies, Retrieved 25/8/2021. Edited.
  2. ^ أ ب ت ث ج "Basic Gates and Functions", ee surrey, Retrieved 24/8/2021. Edited.
  3. ^ أ ب ت "Logic NOR Gate Tutorial", Electronics Tutorials, Retrieved 24/8/2021. Edited.
  4. ^ أ ب Michael Lewin (5/6/2012), "ALL ABOUT XOR", accu, Retrieved 25/8/2021. Edited.
  5. ^ أ ب "Exclusive-OR Gate Tutorial", electronics-tutorials.ws, Retrieved 25/8/2021. Edited.
  6. ^ أ ب ت ث "X OR Gate X NOR Gate", RIVERGLENNAPTS, Retrieved 24/8/2021. Edited.
  7. ↑ "XOR and XNOR", DIGILENT, Retrieved 24/8/2021. Edited.
  8. ^ أ ب "Logic Gates", tutorialspoint, Retrieved 25/8/2021. Edited.
6880 مشاهدة
للأعلى للسفل
×