قانون كولوم في الفيزياء

التعريف بقانون كولوم

يعرّف قانون كولوم (Coulomb’s Law) بأنّه القانون الذي يحسب القوّة الكهربائيّة التي تؤثّر بها الشحنات الكهربائيّة على بعضها،^[١] ويُنسب اكتشاف القانون لعالم الفيزياء الفرنسي شارل أوغستان دي كولوم في نهايات القرن الثامن عشر والذي سمّي القانون باسمه فيما بعد.^[٢]

استعان كولوم بجهاز يسمّى بميزان اللّي (Torsion Balance) للوصول إلى هذا القانون، ووجد تجريبيًا تكوّن قوّة كهربائيّة بين الجسميات المشحونة; حيث أنّ الجسيمات ذات الشحنات المتشابهة تنشأ بينها قوى تنافر، أمّا الجسيمات ذات الشحنات المختلفة فينشأ بينها قوى تجاذب.^[٣]

نص قانون كولوم وشرحه

ينصّ قانون كولوم على أنّ القوّة الكهربائيّة المتبادلة بين شحنتين كهربائيتين تتناسب طرديًّا مع مقدار هاتين الشحنتين، وعكسيًا مع مربّع المسافة الفاصلة بينهما، ويطبّق قانون كولوم إمّا على الشحنات الكهربائيّة أو على الجسيمات الكرويّة المشحونة والتي تتمركز شحنتها في مركزها.^[٣]

يعني ذلك أنّ أيّ جسيمين مشحونين أو شحنتين كهربائيتين تؤثّر كل منهما على الأخرى بقوّة كهربائيّة متساوية، ولكنّ اتجاه التأثير يكون معكوسًا وذلك حسب قانون نيوتن الثالث والذي ينصّ على أنّ لكلّ فعل ردّ فعل مساوٍ له في المقدار ومعاكس له في الاتجاه، ومنه فيمكن اعتبار أنّ تأثير الشحنة الأولى على الثانية هو قوّة الفعل، وردّ الفعل يكون هو تأثير الشحنة الثانية على الأولى ويكون اتجاه التأثير عكس اتجاه قوّة الفعل، وتتأثّر هذه القوّة بعدّة عوامل رئيسيّة كما يأتي:^[٣]

• مقدار كلّ من الشحنتين الكهربائيتين (شـ1، شـ2) ، بعلاقة طرديّة.
• سماحيّة الوسط الكهربائيّة (Permittivity of Space) والتي يرمز لها بالرمز (ε)، بعلاقة عكسيّة.
• مربّع المسافة الفاصلة بين الشحنتين (ف²)، بعلاقة عكسية.

الصيغة الرياضية لقانون كولوم

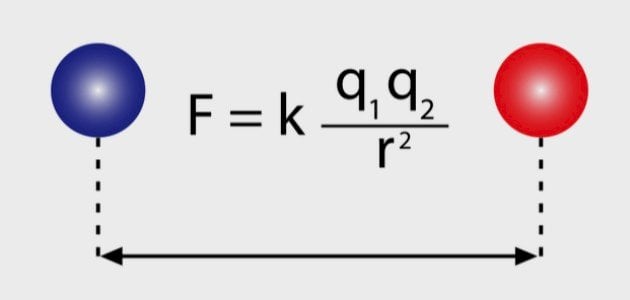
يمكن التعبير عن قانون كولوم رياضيًا كالآتي:^[٤]

ق = أ (شـ1 شـ2) / ف²

حيث تمثّل هذه الرموز ما يأتي:^[٣]

• ق و F: هي القوة الكهربائية المتبادلة وتقاس بوحدة نيوتن.
• أ و A: هو ثابت التناسب ووحدته هي نيوتن.م²/ كولوم²، وهو مقدار يعتمد على سماحيّة الوسط الكهربائيّة (ε).
• شـ1 شـ2 و q1 q2: هي مقدار كل من الشحنة الأولى والشحنة الثانية، ووحدتها الكولوم.
• ف و d: هي المسافة الفاصلة بين كل من الشحنتين، ووحدتها المتر.

كما يمكن كتابة قانون كولوم بصيغة تفصيليّة بناءً على ما سبق كالآتي:^[٣]

ق = 1/(4πε) × (شـ1 شـ2) / ف²

تطبيقات حياتية على قانون كولوم

يوجد العديد من التطبيقات الحياتيّة اليوميّة وأخرى تكنولوجيّة عمليّة لقانون كولوم، ومن هذه التطبيقات ما يأتي:^[٥]

• الطلاء الإلكتروستاتيكي: يُستخدم هذا النوع من الطلاء أثناء عمليّة طلاء السطوح المعدنيّة كالسيّارات، ويقوم على مبدأ ردّ رشّ رذاذ الطلاء والذي يحمل شحنات موجبة على السطح المراد طلاؤه والذي يحمل شحنات سالبة، مما يؤدّي لتوزيع منتظم لمادّة الطلاء على الجسم.
• ذوبان ملح الطعام في الماء: حيث أنّ ملح الطعام مركّب قطبيّ يؤدّي لتفاعل إليكتروستاتيكي ما بين أيونات المُذاب والمذيب السالبة والموجبة.
• قضيب الزجاج المشحون: عند فرك قضيب زجاج بنوع من أنواع القماش كالصوف او الحرير، فإنّه يكسب شحنة كهربائيّة ويصبح ذو صفات كهربائيّة ويتفاعل بقوى التجاذب والتنافر مع الأجسام القريبة منه.
• تنقية الهواء الإلكتروستاتيكية: حيث تتأيين جزيئات الأغبرة والدخان الموجودة في الهواء عن طريق مرورها عبر خليّة كهربائيّة مشحونة فتُشحن هذه الحزيئات، ومن ثمّ تدخل هذه الأغبرة والأدخنة إلى وحدة تحمل شحنات كهربائيّة مخالفة فتنشأ قوى تجاذب تؤدّي إلى تجميع هذه الأدخنة وتنقية الهواء منها.
• شحن مشط الشعر: عند تمرير مشط الشعر عبر الشعر فإنّه يكتسب شحنة كهربائيّة، فيصبح قادرًا على جذب جسيمات أخرى صغيرة تعاكسه في الشحنة كقصاصات ورقيّة.
• الطباعة الجافّة: وهي طريقة طباعة تعتمد بشكل أساسيّ على زيادة الموصليّة الكهربائيّة للمواد عند تعرّضها للضوء، وتجاذب مواد الطباعة والورق والذي يحمل كلّ منهم شحنات متعاكسة مما يؤدي لنزول مواد الطباعة على الورق.^[٦]

مسائل تدريبية على قانون كولوم

إذا كانت الشحنتين والمسافة بينهما معلومة

إذا عُلِم أنّ شـ1 = -4 × 10⁻⁴ كولوم، شـ2 = 20 × 10⁻⁵، يفصل بينهما مسافة 60 سم، ما مقدار القوّة المؤثّرة المتبادلة بين الشحنتين وما نوع القوّة بينهما؟ الحلّ:

• ق = أ (شـ1. شـ2) / ف²
• ق = 9×10⁹ (4 × 10⁻⁴) ( 20 × 10⁻⁵) / (60 × 10^-2)²
• ق = 2000 نيوتن.
• ونوع القوّة بين الشحنتين هي قوّة تجاذب، لأنّ نوع الشحنتين مختلف.

إذا كانت القوة والمسافة معلومين والشحنتين مجهولات

جُسيمان كرويّان صغيران مشحونان، يحمل إحداهما ثلاث أمثال شحنة الجسيم، والمسافة الفاصلة مركزيهما هي 5 أمتار، فما مقدار شحنة هاذين الجسيمين إذا كانت القوّة الكهربائيّة المتبادلة بينهما تساوي 9 نيوتن؟ الحلّ:

• نفرض شـ1 = شـ، ومنه شـ2 = 3 شـ.
• ق = أ (شـ1 شـ2) / ف²
• ق = 9×10⁹ (شـ × 3 شـ) / ف²
• 9 = 9×10⁹ شـ² / (5)²
• شـ = ± (1.581 × 10⁻⁴) كولوم وهي قيمة الشحنة الأولى، وتُهمل الشحنة الموجبة، لأنّ الشحنتين سالبتين من الفرض.
• ولأنّ الشحنة الثانية تساوي 3 أمثال الشحنة الأولى فإنّ:
• شـ2 = 3 (1.581 × 10⁻⁴) = 4.743 × 10⁻⁴ كولوم.

إذا وجِدت 3 شحنات ضمن مسافات مختلفة

ثلاث شحنات كهربائيّة موضوعة على استقامة واحدة، حسب المعلومات الآتية:

• الشحنة الأولى (شـ1) من اليمين قيمتها 4 نانو كولوم.
• الشحنة الثانية (شـ2) تقع في منتصف المسافة بين الشحنتين الأُخريتين، وقيمتها -12 نانوكولوم.
• الشحنة الثالثة (شـ3) تبعد عن الشحنة الأولى مسافة 6 سم، -12 نانوكولوم.

بناءً على ما سبق، ما هي القوّة الكهربائيّة المحصّلة المؤثّرة على الشحنة الأولى (شـ1)، وما هو اتجاهها؟

الحلّ:

• شـ1 = (4 × 10⁻⁹) كولوم، شـ2 = شـ2 = (-12 × 10⁻⁹) كولوم كولوم، شـ3 = (-12 × 10⁻⁹) كولوم.
• نجد القوّة الكهربائيّة التي تؤثّر بها الشحنة الثانية على الأولى كالآتي، ق12 = أ (شـ1 شـ2) / ف².
• ق12 = 9 × 10⁹ × (4 × 10⁻⁹) (-12 × 10⁻⁹) / (3 × 10⁻²)².
• ق12 = (48 × 10⁻⁵) نيوتن، باتجاه محور السينات السالب، لأنّ القوة هي قوّة تجاذب.
• نجد القوّة الكهربائيّة التي تؤثّر بها الشحنة الثالثة على الأولى كالآتي، ق13 = أ (شـ1 شـ3) / ف².
• ق13 = 9 × 10⁹ × (4 × 10⁻⁹) (-12 × 10⁻⁹) / (6 × 10⁻²)².
• ق13 = (12 × 10⁻⁵) نيوتن، باتجاه محور السينات السالب، لأنّ القوة هي قوّة تجاذب.
• نحسب القّوة المحصّلة المؤثّرة على شـ1 كالآتي:
• ق المحصّلة = ق12 + ق13.
• ق المحصّلة = (48 + 12)(10⁻⁵).
• ق المحصّلة = (60 × 10⁻⁵) نيوتن، باتجاه محور السينات السالب.

الملخّص

ينصّ قانون كولوم على أنّ القوّة الكهربائيّة المتبادلة بين أي شحنتين كهربائيتين تتناسب طرديًا مع مقدار كل من الشحنتين وعكسيّاً مع مربّع المسافة الفاصلة بينهما، كما تتنافر الشحنات المتشابهة، وتتجاذب الشحنات المختلفة، ولهذا القانون العديد من التطبيقات الحياتية والعمليّة والتكنولوجية المختلفة والمهمة.

المراجع

1. ↑ "Coulomb's Law", physics classroom, Retrieved 3/9/2021. Edited.
2. ↑ "Charles-Augustin de Coulomb", britannica, Retrieved 31/8/2021. Edited.
3. ^ ^{أ ب ت ث ج} physics for scientists and engineers, Page 711-715. Edited.
4. ↑ "Coulomb's Law", hyperphysics, Retrieved 30/8/2021. Edited.
5. ↑ "8 Coulomb’s Law Examples in Daily Life", studiousguy, Retrieved 3/9/2021. Edited.
6. ↑ "Chester Carlson and Xerography", xerox, Retrieved 3/9/2021. Edited.