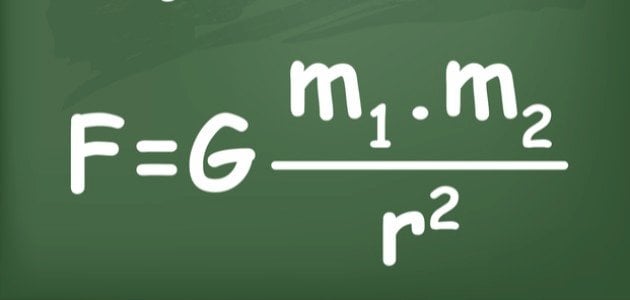قوانين نيوتن للجاذبية

قانون الجذب العام لنيوتن

يًعدّ قانون الجذب العام أو قانون التجاذب الكوني (بالإنجليزية:Newton's Law of Universal Gravitation) واحدًا من أبرز إنجازات نيوتن، وأكثرها أهميّة، وهو من القوانين الفيزيائيّة الاستنباطيّة.^[١]

وينص قانون الجذب العام على أنه "يوجد قوّة جذب بين أي جسمين من أجسام الكون؛ إذ يتناسب مقدار هذه القوة طرديًّا مع حاصل ضرب كتلتيّ هذين الجسمين، وعكسيًا مع مربع المسافة الفاصلة بين المركزين"، ومن هنا فإنّ قانون الجذب العام يُطلق عليه أحيانًا قانون التربيع العكسيّ، وبناءً على هذا القانون فإنّ كل كتلة من الكتلتين تؤثّر على الكتلة الأخرى بقوّة معينة.^[١]

ويمكن صياغة القانون رياضيًا كالتالي:^[١]

قوة الجذب = ثابت الجاذبية (كتلة الجسم الأول × كتلة الجسم الثاني)/ مربع المسافة بين الجسمين

وبالرموز:

ق ج = ج (ك1 × ك2) / ف²

وبالإنجليزية:

F = G (m1× m2) / R²

إذ إن:

• ق ج (F): قوة الجذب، بوحدة نيوتن.
• ج (G): ثابت الجاذبية، وتبلغ قيمته 6.67×10^-11 نيوتن. كغ^-2.م²
• ك1 (m1): كتلة الجسم الأول، وتقاس بوحدة كغ.
• ك2 (m2): كتلة الجسم الثاني، وتقاس بوحدة كغ.
• ف²:مربع المسافة بين الجسمين، بوحدة م.

أمثلة متنوعة على قانون الجذب العام لنيوتن

وفيما يأتي أمثلة متنوعة على قانون الجذب العام لنيوتن:

حساب قوة الجذب بين الأرض والقمر

تبلغ كتلة الأرض 10²⁴×6.0 كغم، وكتلة القمر 10²²×7.35 كغم، ومتوسط المسافة بين مركز الأرض ومركز القمر10⁸×3.8 م، ما مقدار قوة الجاذبية بين الأرض والقمر؟ استخدم ج= ^11-10×6.67 لقيمة ثابت الجذب العام، واكتب الإجابة بالصيغة العلمية لأقرب منزلتين عشريتين.

• المعطيات:
  • كتلة الأرض (ك1)= 6.0×10²⁴
  • كتلة القمر (ك2)= 7.35×10²²
  • مربع المسافة= ²(3.8×10⁸)
  • ثابت الجذب العام= 6.67×10^-11

• الحل: نعلم أن الجاذبية تؤثِّر بقوة متساوية على كل من الأرض والقمر، وتؤثِّر هذه القوة على طول الخط المستقيم الذي يصل بين مركزَي كتلتَي الجسمين؛ أي بين مركز الأرض ومركز القمر، وبتطبيق المعطيات في معادلة الجذب العام: ق ج = ج (ك1 × ك2) / ف² :
  • ق ج = 6.67×10^-11 [(6.0×10²⁴×7.35×10²²)] /²(3.8×10⁸)
  • ق ج = (6.67×6.0×7.35) (^11-10ײ⁴10ײ²10) / (3.8×3.8) (10⁸×10⁸)
  • ق ج = 294.147×10³⁵ / 14.44×10¹⁶
  • ق ج = 20.37 × 10¹⁹ نيوتن.
  • ق ج = 20.037 × 10²⁰ نيوتن.

حساب المسافة بين جسمين بمعرفة قوة الجاذبية بينهما

جسمين كتلة الجسم الأول 4.6 كغم، وكتلة الجسم الثاني 2.9 كغم، وكان مقدار قوة الجاذبية بين الجسمين ^10-10× 3.2 نيوتن، ما مقدارالمسافة بين الجسمين؟ علمًا أن قيمة ثابت الجذب العام (ج= ^11-10×6.67)، اكتب الإجابة بالصيغة العلمية لأقرب منزلتين عشريتين.

• المعطيات:
  • كتلة الجسم الأول (ك1) = 4.6 كغم
  • كتلة الجسم الثاني (ك2) = 2.9 كغم
  • قوة الجاذبية بين الجسمين ( ق ج) = 3.2 × 10^-10 نيوتن.
  • ثابت الجذب العام (ج) = 6.67×10^-11

• الحل
  • بتطبيق المعطيات في معادلة الجذب العام: ق ج = ج (ك1 × ك2) / ف²
  • 3.2 × 10^-10 = 6.67×10^-11 ( 4.6× 2.9) / ف²
  • ف² = 6.67×10^-11 ( 4.6× 2.9) / 3.2 × 10^-10
  • يُأخذ الجذر التربيعي للمعادلة لإيجاد المسافة وليس مربع المسافة، ومنه: ف = 1.6675 م

تطبيقات على قانون الجذب العام

ينطبق قانون نيوتن للجذب العام على الأجسام الموجودة سواء أكانت على مسافات كبيرة جدًا، مثل الأجرام الفلكية التي تمتلك كتلة كبيرة مثل الشمس؛ والأرض؛ والقمر، وكذلك ينطبق قانون نيوتن على المسافات القصيرة أيضًا مثل المسافة بين التفاحة وسطح الأرض، ولكن القانون لا يمكن تطبيقه إذا كانت المسافة بين الجسمين أقل من ^9-10 م.^[٢]

وفيما يأتي أبرز تطبيقات قانون الجذب العام لنيوتن:

الجاذبية الأرضية 

تُظهر قوانين نيوتن في الحركة أن الأجسام في حالة السكون ستبقى في حالة سكون والأجسام المتحركة ستستمر في التحرك بشكل موحد في خط مستقيم ما لم يتم التأثير عليها بقوة، ومن هنا فإن الخط المستقيم هو الذي يحدد حالة الحركة الطبيعية.^[٣]

ولكن الكواكب تتحرك في شكل بيضاوي وليس في خطوط مستقيمة، وبالتالي يجب أن تكون هناك قوة تؤثر على مسارات الكواكب، وبهذا اقترح نيوتن أن تلك القوة هي الجاذبية الأرضية.^[٣]

وفي زمن نيوتن، كانت الجاذبية شيئًا مرتبطًا بالأرض فقط، ولكن توضح التجارب اليومية التي نعيشها أن للأرض قوة جاذبية على الأجسام الموجودة على سطحها، فمثلًا إذا سقط شيء ما، فإنه ينجذب نحو الأرض عندما يسقط.^[٣]

وقد كانت رؤية نيوتن هي أن الجاذبية الأرضية يمكن أن تمتد حتى القمر وتنتج القوة المطلوبة للتأثير على مسار القمر من خط مستقيم إلى بيضاوي وتحافظ على إبقائه في مداره، فهو يفترض أن الجاذبية لا تقتصر على الأرض فقط، وإنما هناك قوة جذب عامة بين جميع الأجسام المادية مثل؛ قوة الجاذبية بين الشمس والكواكب.^[٣]

الجاذبية في النواة

لفهم الجاذبية في النواة بشكل علمي دقيق، لابد من التطرق لقوى الجذب الأربعة التي تجعل الذرة متماسكة، وهي:^[٤]

• القوة المغناطيسية

وهي المسؤولة عن تجاذب الجسيمات موجبة الشحنة مع الجسيمات سالبة الشحنة، إذ تتجاذب الإلكترونات ذات الشحنة السالبة، مع البروتونات ذات الشحنة الموجبة، ما يحافظ على دوران الإلكترونات في مدار ثابت حول النواة.

• القوة النووية القوية

يوجد داخل نواة الذرة البروتونات موجبة الشحنة، وحسب القوة المغناطيسية يجب أن تتنافر هذه الجسيمات، وهذا إن حدث ستنفجر جميع الذرات في الكون، ولكن بفضل القوة النووية القوية، فإنها تحافظ على البروتونات متماسكة، وتعمل القوة النووية القوية مع القوة المغناطيسية على تماسك الذرة.

• القوة النووية الضعيفة

وهي القوة المسؤولة عن تماسك الجسيمات داخل الذرة مع بعضها البعض، من خلال عملية الاضمحلال الإشعاعي، التي يتحوّل النيوترون فيها إلى بروتون وإلكترون.

• قوة الجاذبية

وتعتبر أضعف القوى الأربع التي تحافظ على الذرة متماسكة، ولكنها تساهم في جذب الجسيمات لبعضها البعض.

تطبيقات أخرى

وهناك العديد من التطبيقات التي أثبتت صحة قانون نيوتن للجذب الكوني، أبرزها التالي:^[٢]

• إطلاق الأقمار الصناعية الحديثة التي تدور في مدارات حول الأرض، وبقائها ثابتة في مسارها، اعتمدت في إطلاقها على قانون نيوتن للجذب الكوني، وهذا دليل واضح وملموس على صحة هذه النظرية.
• تطبيق العلماء قانون نيوتن للجذب الكوني في تفسير ظاهرتي كسوف الشمس، وخسوف القمر، وهذا دليل آخر على صحة النظرية.
• تفسير العلماء ظاهرتي المد والجز للمسطحات المائية على الأرض، وفقًا لقوة الجذب بين القمر ومياه هذه المسطحات، وهو ما يثبت نظرية نيوتن للجذب الكوني على مسافات كبيرة جدًّا.

المراجع

1. ^ ^{أ ب ت} "Newton's law of gravitation", britannica, Retrieved 30/9/2021. Edited.
2. ^ ^{أ ب} "Universal Law of Gravitation", vedantu, Retrieved 30/9/2021. Edited.
3. ^ ^{أ ب ت ث} "Newton’s Universal Law of Gravitation", lumenlearning, Retrieved 30/9/2021. Edited.
4. ↑ "Forces within the Atom", w3.ric.edu, Retrieved 3/10/2021. Edited.